生存分析简明教程

在生物医学研究中，生存分析 是非常重要和常见的分析方法。本文对 生存分析 中的Kaplan–Meier 模型、Cox 比例风险模型进行了简要而详尽的概述，帮助大家更好的理解生存分析等相关概念。本文适用于生物医学专业初学者以及对生存分析感兴趣的非专业人士。

生存分析

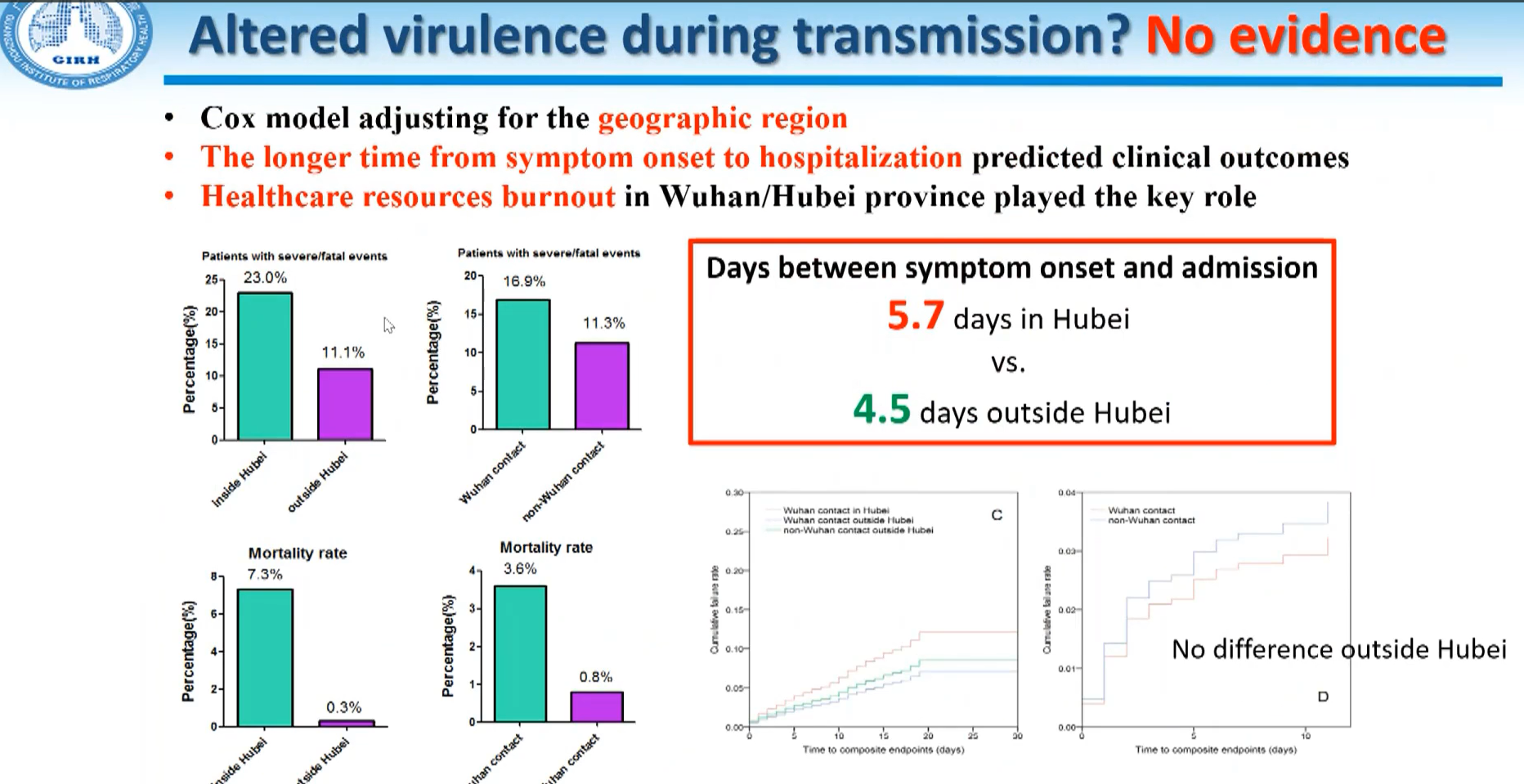
首先，简单描述一下 生存分析 的使用场景，已经熟悉的同学可以选择直接跳过。 生存分析 经常用在癌症等疾病的研究中，例如在对某种抗癌药物做临床试验时，会首先筛选一部分癌症患者随机分为两组，一组服用该试验药物，一组服用对照药物，服药后开始统计每个患者从服药一直到死亡的生存时间，通过考察两组之间的病人在生存时间上是否有统计学差异来判断试验药物是否有效。在这里，死亡是整个实验中重点观测的事件，即 event。对于每个病人，需要记录他们发生该事件的具体时间。因此， 生存分析 可以抽象概述为，研究在不同条件下，特定事件发生与时间的关系是否存在差异。这些具体事件可以是死亡，也可以是肿瘤转移、复发、病人出院、重新入院等任何可以明确识别的事件，而不同条件即为不同的分组依据，可以是年龄、性别、地域、某个基因表达量的高低、某个突变的携带与否等等。下图是钟南山院士在对欧洲呼吸学会针对 Covid-19 的报告中提到的研究结果，他们对湖北省内和省外的病人从开始症状到入院时间做了分析，从发生症状开始，入院则是我们刚才讲的 event 事件，而湖北省内外则是不同的分组条件。图中还提到，他们使用 Cox 模型对地理进行了校正，这也是我们在这篇文章中后续要讲到的内容。对钟南山报告感兴趣的同学可以访问此链接 进行查看。

上面对生存分析的使用场景做了简单介绍，相信大家已经大概对生存分析有了基本的印象。接下来我们需要提前交待一下关于删失数据的情况，即 censored data. 

删失数据，字面意思是删除丢失的数据，它在生存分析里面实际指的是在实验过程中丢失的、失去跟踪的数据。举例来说，对于肿瘤治疗药物的临床试验，关注事件为从服药到死亡，但是有一部分病人在试验过程中会无法观测到死亡事件的发生，比如无法联系到、或主动退出、或其他需要紧急处理退出临床试验的情况、以及试验结束时还未发生死亡等，这些数据就称作删失数据。考虑到这种类型的删失保留了从一开始到删失前的进展，而丢失了后续的结局，我们将这类删失称作右删失。相对应的，还有一种类型叫做左删失，比如我们要统计从初次患病到最终死亡的生存时间的分析，有些病人已知患有疾病且知道其死亡时间，但无法确定初次患病的时间，这样的删失则成为左删失。对于左删失数据，有一些对应的方法进行处理，我们这里不做讨论（有时间的话可以加进来）。本文后续主要对右删失的情况进行考虑。

开始之前，我们再明确两个概念。1，生存概率，即 Survival probability，指的是研究对象从试验开始直到某个特定时间点仍然存活的概率，可见它是一个对时间t的函数，我们定义之为 S(t)；2，风险概率，即 Hazard probability ，指的是研究对象从试验开始到某个特定时间 t 之前存活，但在 t 时间点发生观测事件如死亡的概率，它也是对时间 t 的函数，定义为 H(t)。接下来要讲的 Kaplan-Meier 方法主要关注 S(t)，而后面讲到的 Cox 风险比例模型则关注 H(t)。

下面进入正题，引入 Kaplan–Meier 方法，该方法是由 Kaplan 和 Meier 与 1958 年共同提出的，为理解方法的细节，我们先看下一张表(原文链接)。本例中我们以死亡作为观测事件，这张表也叫做 life table.

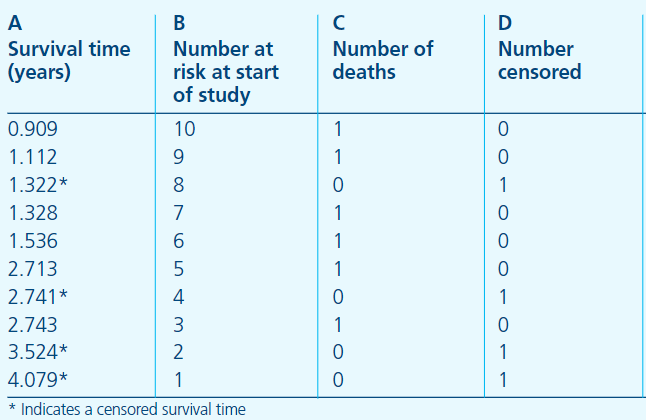
 A 列是从试验开始起，持续的观测时间，星号代表在该时间有删失数据发生；B 列是指在 A 列对应的时间开始之前所有存活的研究对象个数，也可以叫做 at risk 的人数，表示当前具有死亡风险的有效人群，是排除了已经死亡和删失的数据之后剩余的人数；C 列为恰好在 A 列对应的时间死亡的人数，D 列即表明在该时间点删失的个数。第一行则可以解读为，在 0.909 年这个时间点之前，本来有 10 个患者，在 0.909 这个时间点（或其之后的一小段时间区间）死亡了一个人，没有删失数据，意味着还剩 9 人；随后，只要有新增死亡或删失数据，则在表中新建一行，记录时间和人数。

我们先不引入 Kaplan–Meier 公式，大家可以先尝试自己去思考下如何计算每个时间节点的生存概率，即 S(t)。比如在 1.536 年这个时间点，即表中的第五行，病人在该点的生存概率是多少呢？很容易可以想到，要想在 1.536 这个时间点存活，他/她必须在 1.536 之前的所有时间点存活才行，也就是说在 0.909、1.112、1.322、1.328 这几个时间点，病人都必须存活。那么在 1.536 这个时间点的生存概率 P 实际上就等于在包括 1.536 在内的所有之前的时间点都不死亡的概率乘积，即：

P(存活至1.536) = P(0.909时不死亡) * P(1.112时不死亡) * P(1.322时不死亡) * P(1.328时不死亡) * P(1.536时不死亡)

对于某个特定时间点不死亡的概率，可以用 1 – 死亡概率 来估算，举个例子：

P(0.909时不死亡) = 1 – P(0.909时死亡) = 1 – (0.909时死亡的人数)/(0.909之前的所有人数) = 1 – 1/10 = 0.9

P(1.112时不死亡) = 1 – P(1.112时死亡) = 1 – (1.112时死亡的人数)/(1.112之前的所有人数) = 1 – 1/9 = 0.89

需要注意的是，删失数据发生时，由于当前时间点没有发生死亡人数，该时间点对累计的生存概率不产生贡献。但由于总人数减少，会对下一个时间点的生存概率产生影响。如：

P(1.322时不死亡) = 1 – P(1.322时死亡) = 1 – (1.322时死亡的人数)/(1.322之前的所有人数) = 1 – 0/9 = 1

当我们计算出每个时间点不死亡的概率之后，我们就可以通过连续乘积算出每个时间点的生存概率，即存活至该时间点的概率。如下表所示：

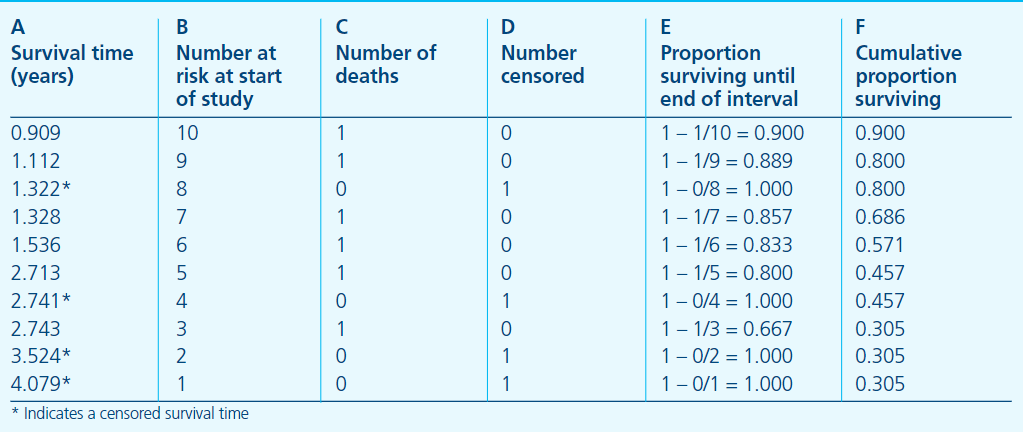
该表中  E 列即不死亡概率，F 列则表示累积的生存概率，可以看到随着时间增加，死亡人数增多，越到后期，生存概率越低，这是符合常理的。另外需要注意，在删失发生时，生存概率时没有变化的。

其实我们刚才的思路就是 Kaplan–Meier 方法的主要思路，基于刚才的表格，我们也可以用数学公式来表示。一共有 m 个时间点，每个时间点用下标 i 来表示, i 为从 1 到 m 的整数, 生存概率 S(t_i) 可以表示为：

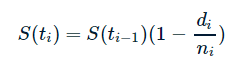
其中，t_i 表示第 i 个时间点，n_i 表示在 t_i 之前的有效人数，d_i 表示在 t_i 死亡的人数，S(t_i-1) 表示在上一个时间点 i-1 的生存概率。

根据这一公式，我们可以画图来展示生存率的变化情况，即 Kaplan-Meier 生存曲线，如下图所示：

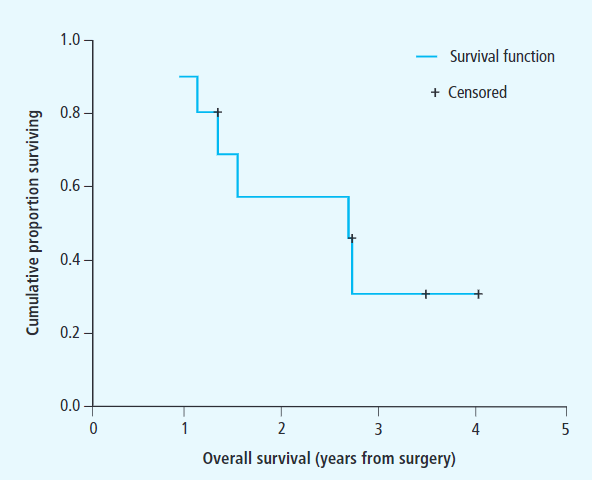
图中横轴即时间轴，纵轴是累积存活比例，也就是生存概率，加号表示删失数据。一般来说，生存分析是要比较不同组之间的一个生存情况，因此 Kaplan-Meier 生存曲线一般不止一条曲线，如下图所示：

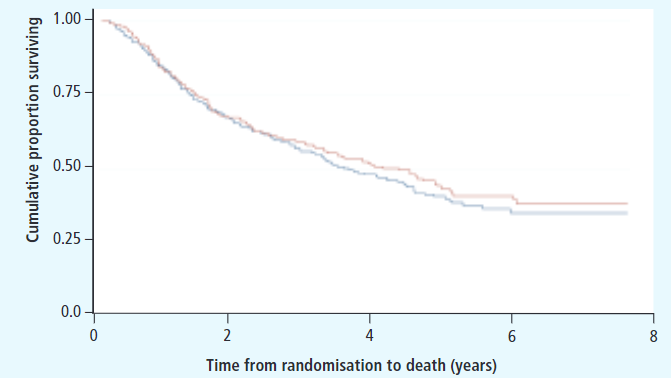
图中不同颜色表示不同的两组病人，在时间轴上生存情况的不同表现。该图中，红色和蓝色的线基本上重叠在一起，后期红色线稍微高一点，也就是说红色组的后期生存概率更高，病人死亡的相对慢一点。可以想象，如果某一组的生存情况特别差，那么它的生存曲线应该是一条极速下降的阶梯状。然而我们知道，在统计学中必须要有量化的指标来衡量差异及其显著性，不能仅通过观测来确定两组之间是否存在差异。

最直观的是来统计中位生存时间，即生存率在 50% 时所对应的生存时间，如下图所示：

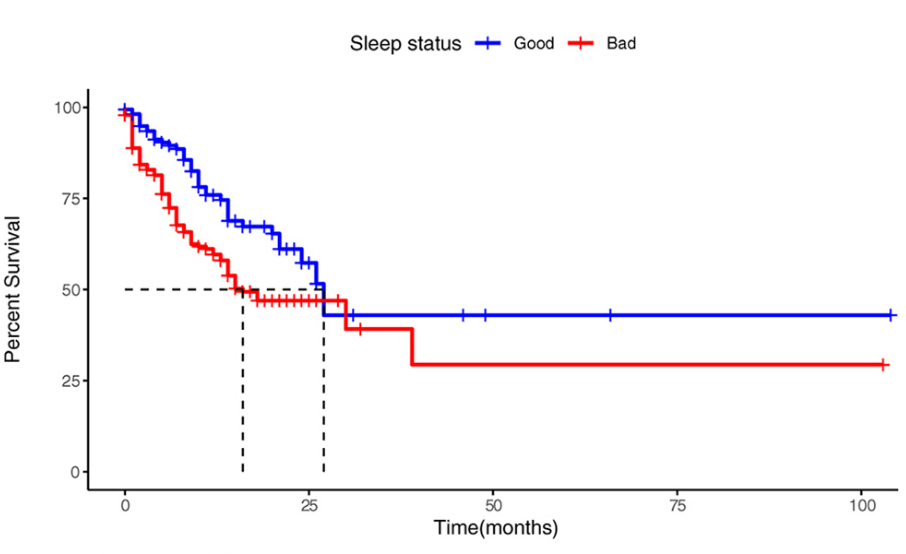
不同组别对应的中位生存时间不同，可以一定程度上反应出不同组别死亡风险的不同。如果想比较整体生存时间分布是否存在统计学差异，一般我们可以采用 Logrank 统计方法来对生存数据进行统计分析。

Logrank 方法是由 Nathan Mantel 最初提出的，它是一种非参数检验，中文翻译为对数秩检验，主要用来比较两组样本的生存时间分布的差异。Logrank 实际计算形式可能有不同的变体，我们这里介绍一种版本，实际上是卡方检验的一种应用场景。Logrank 检验的零假设是指两组的生存时间分布完全一致，当我们通过计算拒绝零假设时，就可以认为两组的生存时间分布存在统计学差异。我们可以通过以下公式计算某组病人在某个时间点的期望死亡人数：

E_1t = N_1t*(O_t/N_t)

其中 E_1t 是指第一组中，在时刻 t，期望死亡人数；N_1t 指第一组中 t 时刻 at risk的人数，即 t 之前的存活人数；O_t 则指两组（第一组和第二组）总的观测到的实际死亡人数；N_t 指两组总的 at risk 的人数，或 t 时间之前两组的总人数。如果你认真观察了公式，你就会觉得它其实浅显易懂，因为两组生存概率分布一致，因此两组总的 at risk 人数和两组总的死亡人数的比例，应该和单组的 at risk 人数和总死亡人数的比例是一致的，这也就是为什么通过两组总的比例和其中一组总的 at risk 的人数，就可以得到这一组期望死亡的人数，也就是上面公式所讲的内容。

有了每个时间点的死亡期望值之后，我们构造如下的卡方值：

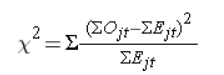
在该公式中，外层的 Σ 是对不同组的一个叠加，内层的三个 Σ 都是对不同时间点的叠加；j 代表的是第 j 组，比如服药组和对照组就可以分别对应 j=1 和 j=2 ；这里分子上的 ΣO_jt 是指在 j 组所有时间点的观测死亡人数相加之和，是对不同时间点 t 对应的观测值的一个累加，比如 t 分别对应 1 天、2 天、3 天等等；ΣE_jt 是指在 j 组所有时间点期望死亡人数相加之和。观测人数和期望人数的差值，就代表了实际情况与我们假设情况是否一致，如果假设是对的，即不同组的生存时间分布是完全一致的，那么观测人数和期望人数的差值会是非常小的。因为差值有正有负，所以对它取平方，这样就不会出现抵消的情况。另外，由于 100 和 120 之间相差的 20，和 1000 和 1020 之间相差的 20，情况并不完全一样，100 和 120 之间的 20 占比达到 20%，而 1000 和 1020 之间相差的 20 占比只达到了 2%，为了让这两种情况可比较，再加一个分母即 ΣE_jt，相当于转换成百分比；最后把不同组别得到的值加起来，就得到 X² 值。通过查表可根据 X² 值来判断是否需要拒绝零假设。具体的一个手动计算流程可以参考：链接.

除 Logrank 检验之外，一种生存时间分布的常用检验包括 Breslow 检验，其实也就是 Wilcoxon 检验，与 Logrank 不同的是，在每个时间点统计观测人数和期望人数时，他会给它们乘以一个权重因子，即当前时间点的 at risk 的总人数，然后再把所有时间点加起来去统计卡方值。可以想象随着时间点越靠后，at risk 的总人数会越小，因此权重越少，对 X² 值的贡献就越小。因此 Breslow 检验对试验前期的差异要更加敏感，而相对来说 Logrank 对后期相对更敏感一些，因为它的所有时间点的权重参数都是1. 在实际使用中，我们可以使用不同的方法从多个角度对数据去进行探究。

说到这里，Kaplan–Meier 的多数知识我们已经覆盖到了。但还有一个方面可能会引起同学们的注意，如下图所示：

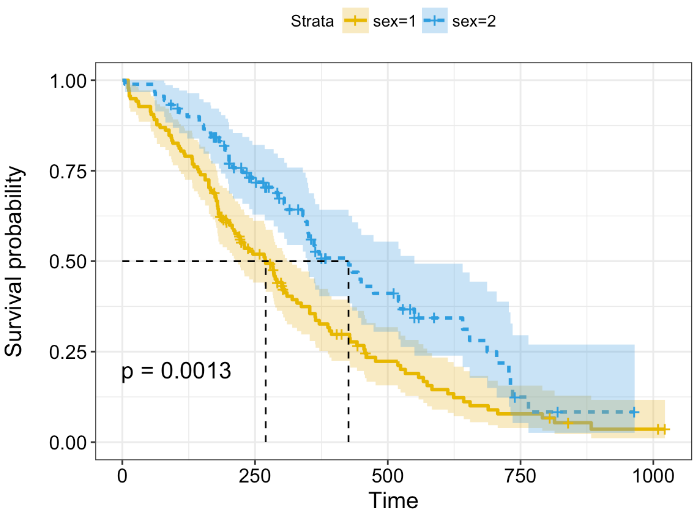
大家可能会问，上图中生存曲线周围的浅色区间是什么？实际上，上图中生存曲线周围的浅色区间即其对应的 95% 置信区间。首先我们需要理解为什么每个节点的生存概率会存在置信区间，因为我们假设每个时间点的生存概率是符合一种特定的分布，那么每次观测到某个时间点的结果就相当于是一次随机抽样，因为我们已经知道了生存概率对于时间 t 的函数 S(t)，通过估算标准误，我们就可以估算出某个时间点的误差范围 (Margin of Error) ，从而得到一个特定概率的置信区间。

针对生存概率分布数据的置信区间估计，一种基于 Greenwood 提出的公式为：

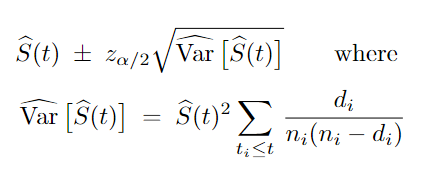
其中 S(t) 即为生存概率函数，是我们之前解释过的不死亡概率的累计乘积。Z_a/2 是 正态分布的 α/2-th 分位数，可以查表得到。

除了上面公式提到的置信区间计算方法，还有一种指数型 Greenwood 公式，可以解决之前计算的置信区间可能不在 (0,1) 区间的问题，两个公式的具体内容和推导都可以参考链接.

到目前为止，我们已经讲了生存分析的基础知识，包括生存分析应用场景、删失数据说明、生存概率和风险概率、Kaplan–Meier 曲线、LogRank 和 Breslow 检验以及置信区间估计。但我们以上讲解的内容都是只针对单变量的，也就是说 Kaplan-Meier、LogRank 只能针对单一的变量进行分析，要么按性别分组，要么按不同药物分组，但无法同时考察多个因素，或对某些可能有影响的因素进行调整。比如我们要考察新冠病毒在湖北省内外的预后差异，假设我们不知道任何其他信息，但有理由怀疑湖北省和其他省份的人口成分可能存在差异，比如湖北省老人更多、儿童更多（假设），那我们就不能直接简单的拿湖北的病例和其他省的病例去比较，必须同时考虑年龄、性别的影响，也就是说要对年龄、性别做出调整，这是之前用 LogRank无法做到的，此时 Cox 比例风险回归模型就要闪亮登场了。

Cox model

下面我们讲解 Cox 比例风险回归模型，英文名叫 Proportional Hazards Regression analysis 或 Cox Proportional-Hazards Model， 是由 Cox 于 1972 年提出的。我们这里简称其为 Cox 模型。

Cox 模型是一种半参数模型，因为它的公式中既包括参数模型又包括非参数模型。简单说下参数模型和非参数模型的相同与区别。相同点是它们都是用来描述某种数据分布情况的；不同点在于，参数模型的参数是有限维度的，即有限个参数就可以表示模型分布，比如正态分布里的均值和标准差；而非参数模型的参数则属于某个无限维的空间，无法用有限参数来表示，不同的数据会得到不同的分布估计，比如决策树、随机森林等等，我们无法用有限的参数来表示所有可能的分布情况。来看看 Cox 模型的公式就知道为什么 Cox 模型是一种半参数模型了。

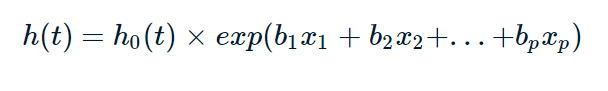
其中 t 是生存时间，x₁, x₂ 到 x_p 指的是具有预测效应的多个变量，b₁, b₂ 到 b_p 则是每个变量对应的 effect size 即效应量，可以理解为结果的影响程度，后面会解释。h(t) 就是不同时间 t 的 hazard，即风险值。而 h₀(t) 是基准风险函数，也就是说在其他协变量 x₁, x₂, …, x_p 都为 0 时，即不起作用时，衡量风险值的函数。根据公式我们可以看到指数部分是参数模型，因为其参数个数有限，即b₁, b₂ 到 b_p，而基准风险函数 h₀(t) 由于其未确定性，可根据不同数据来使用不同的分布模型，因此是非参数模型。所以说, Cox 模型是一种半参数模型。

一个需要注意的地方在于，并不是所有的生存分析数据都可以用 Cox 模型来分析，它是需要满足一定的假设的，大家可以带着这个疑问继续阅读，我们在文章最后对此会进行讨论。

现在我们知道了风险函数 h(t) 的公式，先解读一下这个公式。h(t) 首先是基于时间变化的，t 是自变量；对于某个病人，不同时间的死亡风险是不一样的，这非常好理解，肿瘤病人肯定是随着病程的进展，复发率、死亡率都会不断提高。我们可以回忆以下之前做 Kaplan-Meier 的那个表格，在最后的时间点生存率也越来越低，意味着风险越来越高。其次除了时间，不同年龄、性别、血压等指征不同的病人，死亡风险也不一样。比如这次的新冠病毒 Covid-19，年纪越大致死率越高，这也就是为什么 Cox 模型要把诸多可能影响生存率的因素都当作协变量引入到公式中去，在该公式中即 x₁, x₂, …, x_p。我们的主要目标是通过一定方法来找到合适的 h₀(t),以及所有协变量的系数 b₁, b₂, …, b_p。实际上cox 模型是需要用到极大似然估计等计算方法，首先构建特定的似然函数，通过梯度下降等方法来求解模型的参数，使得函数求解值最大。这里不对细节进行解读，感兴趣的读者可以参考以下文章：链接1, 链接2, 链接3.

假设我们已经通过计算得到了合适的 h₀(t) 和协变量系数，如何去解读结果呢？我们可以比较某个协变量 x₁ 在不同值时对应的不同风险比(hazard ratio)，这里比较 x₁ 和 x₁+1，即若 x₁ 增加 1 个单位，增加前后的风险比是：

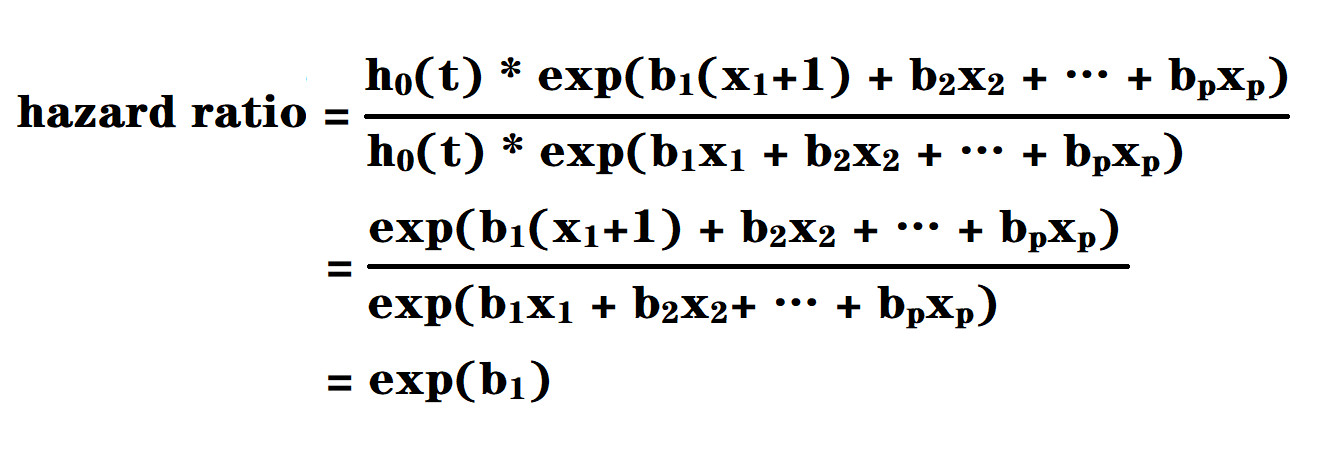
上式中，我们对 x₁+1 和 x₁ 这两个不同的值对应的风险比进行了计算，通过化简可知x₁+1 和 x₁ 对应的风险比实际上等于 exp(b₁)，也就是 e 的 b₁ 次方；简单的讲，假如 x₁ 指的是年龄，那么对于年龄 51岁 (x+1) 和年龄 50 岁 (x) 的人，可能死亡的风险比为 exp(b₁)。如果 b₁>0，则 exp(b₁)>1，意味着年龄 +1，死亡风险增加；如果 b₁<0, 则 exp(b₁)<1，意味着年龄 +1，死亡风险降低；如果 b₁=0，exp(b₁)=1，意味着年龄变化对死亡风险不起作用。

因此，我们知道，对于每一个协变量，如果它的系数为正，表明对应的变量增加时，会增加病人的死亡风险（或其他事件风险，如复发、转移等）；如果它的系数为负，表明对应的变量值增加时，会降低病人的死亡风险。一个具体的计算例子可以查看链接, 一个使用R进行计算的例子可以查看：链接。

下面的表格是一个计算结果：

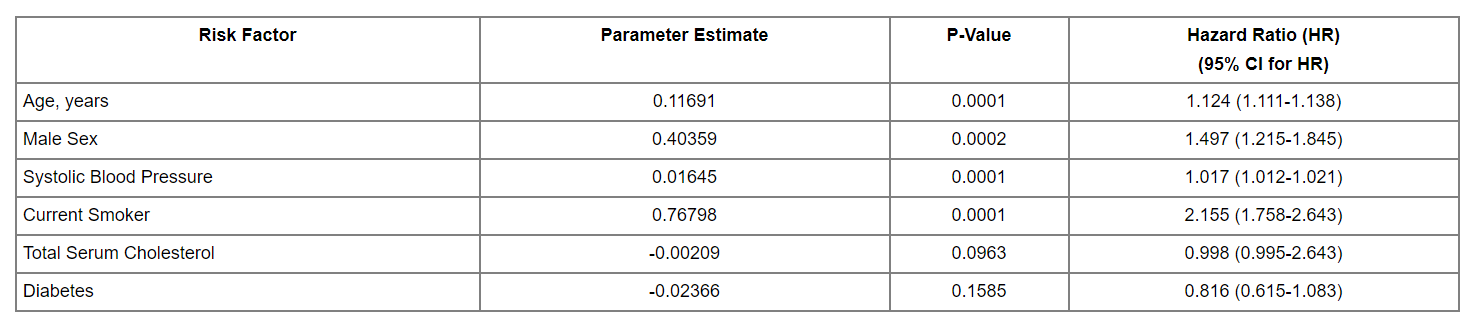
可以看到该表格中，一些风险因子包括年龄、性别、血压（收缩压）、是否抽烟、血清总胆固醇以及是否患有糖尿病，经过 Cox 模型计算，得到各个风险因子的参数估计，如年龄对应的参数为 0.11691，也就是之前公式中的系数为 0.11691，大于 0 表示年龄增加会增加风险，风险比 (hazard ratio) 为 exp(0.11691) = 1.124 ，即表格最后一列，该数值大于 1，同样表明年龄增加会导致风险增加。对于二分类变量，即只有 0 和 1，比如男性为 1，女性为 0，这样的变量与连续变量在 Cox 模型中的结果解读是一致的，如果性别对应的协变量系数大于 0，表明性别值越高风险越大，也就是说男性的风险高与女性。除了关注系数外，同时需要关注的是 p value，即该参数估计是否具有统计学显著性，常用来统计的方法是 Likelihood ratio test，同时也有使用 Wald test, 和 score logrank statistics。简单介绍一下 Likelihood ratio test，中文名叫似然比检验，核心思想是：为了判断都某个新变量的引入是否对于模型有效，比较变量加入前和加入后，似然函数最大值的比较，如果没有出现最大值的降低，那么则可能对模型有效，进而统计其显著性。但这三种统计方法感兴趣的可以查看链接. 

我们之前提到过，使用 Cox 模型是需要满足一定的条件的。相信大家看到这里应该已经有了答案，最重要的一个假设条件是：任意两人的风险比例是不随事件变化的，这也是为什么 Cox 模型全名叫 Cox 比例风险回归模型。举例来说，如果某个人的死亡风险比另一个人高两倍，那么不论什么时候，这个人的死亡风险都是另一个人的两倍。这样的假设我们可以从之前的公式中看到，hazard ratio 推导的结果是不包括时间 t 的。这是 Cox 模型可用的一个基本假设。实际情况并非一定如此，对吧？因此我们在做 Cox 模型之前，最好对数据进行一个解读，看看是否满足当前假设。既然不同人之间的风险比例固定，那么一个最简单的例子就是任意分组情况下，两组的 Kaplan–Meier 曲线不应该相交叉，如果曲线相交叉，说明两组的生存概率关系随事件发生了变化，亦即风险比随时间发生变化，与假设相悖。然而，在实际应用中，由于样本量较小时，生存曲线会引入较大的误差，因此该判断方法有可能失效。一个更加复杂的方法为 complementary log-log plot，即横轴为 ln(t)，纵轴为 ln(-ln(S(t)))。经过推导：

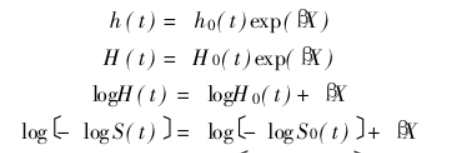
我们可知，不同组中，log(-log(S(t))) 对于 t的曲线，只有 βX 不同，而其与时间 t 无关，所以两条曲线应该近似平行或等距。参考（检查Cox模型比例风险假定的几种图示法_余红梅，链接).

除了画生存曲线观察数据之外，我们还可以通过 Schoenfeld 残差来检查风险是否成比例。具体可以参考链接, 以及检验变量与时间的交互来作用来衡量风险比例是否固定( 链接 )，这里不做展开。对于不符合固定风险比例的数据，可以使用时依协变量或分层Cox模型来计算(链接).

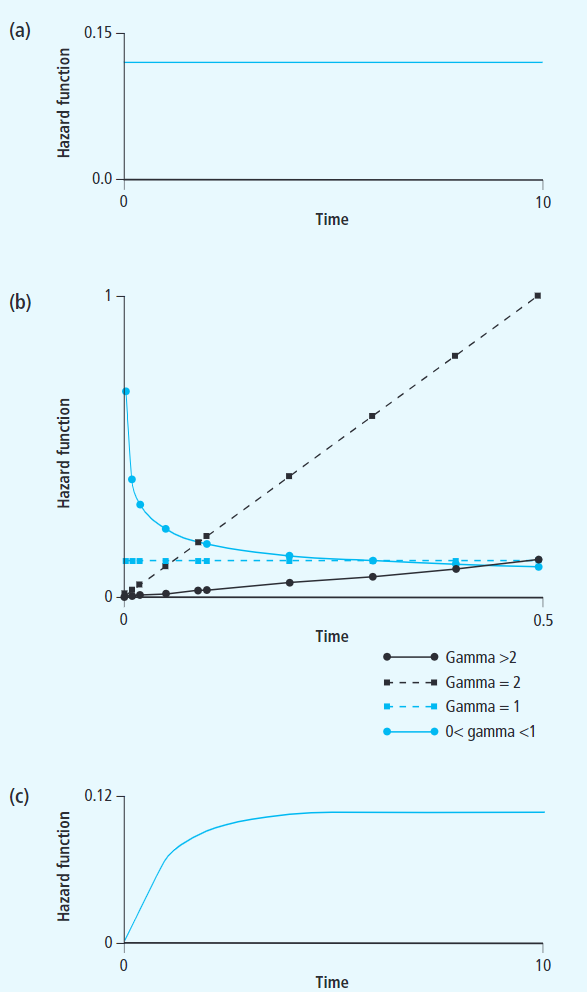
对于 生存分析 ，除了 Cox 模型外，还有一些其他可用的参数模型。与 Cox 模型不同，这些参数模型往往给定了可能的风险函数分布，比如 指数分布、Weibull 和 Gompertz 分布，然后进一步去估计对应的模型参数。如下图所示，a 为指数分布，其 hazard ratio 为恒定值，在实际中很少应用；b 为 Weibull 分布，可通过不同的参数调整分布的走向；c 为 Gompertz 分布。相对于 Cox 模型，使用这些模型的优点在于分布曲线可根据参数推断，可得到更多信息，比如：前期死亡率高后期死亡率低，也就是说可以得到更多关于风险分布的信息，而 Cox 模型只能得到有限信息，如风险比及其显著性。使用这些全参数模型的缺点也是明显的，即固定的分布不一定能满足实际的数据情况，可能带来更多的误差。再实际使用情况中，可根据不同情况进行选择。Weibull 模型的简单介绍可参考链接.

以上, 是对 生存分析 中主要知识的一个大概介绍, 相信大家对于生存分析中的多数概念都有了直观的人数。但由于笔者水平有限，文章可能有表述不清楚、甚至错误的地方，希望读者可以多多提供建议和批评，或者有什么问题可以多多留言讨论，谢谢！

 

---

推荐阅读

简评 Cambly —— 学习语言的捷径还是弯路？

openpbs centos 7 配置手把手教程

理解 Z-Score 标准分数的含义和用法
PyTorch 简明样例：蛋白质序列预测模型构建、数据载入、抽样、训练、评估
wxPython 教程 （译）

Chrome 更新出错？换个思路解决问题！